Abstract

​ 在图像检索过程中，或者ReID(将 Re-ID看作一个检索过程时)，re-ranking是提高其准确性的关键步骤，是各大竞赛刷榜得利器。

​ Re-Ranking的思想基于这么一个假设：

​ if a gallery image is similar to the probe in the k-reciprocal nearest neighbors, it is more likely to be a true match.

​ 简单的解释就是，根据probe在probes+galleries搜索出来的candidate对象，根据这些candidate对象在probes+galleries选择k个nearest，如果包含你的probe，那它的可能性更大一些。

Information

Paper: (CVPR2017) Re-ranking Person Re-identification with k-reciprocal Encoding.

Code:

Reference:

Approach Description

K-reciprocal Nearest Neighbors

​ 回顾常规检索过程，probe(p)在galleries检索的topk({g1,g2,..,}),定义为：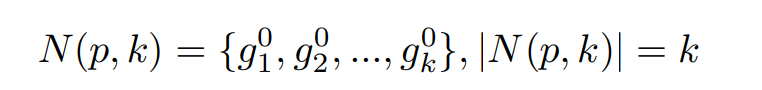

​ k-reciprocal nearest neighbors定义为：

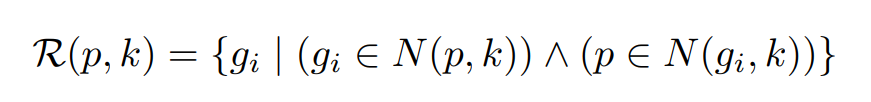
​ probe(p)在probes+galleries检索的topk的candidates对象（不包含p），如果这些candidates对象在probes+galleries选泽的topk包含了p,则该candidate与p互为top-k。

​ 有时候probe的匹配图片不在probe的top-k之中，这时候使用下面的方法进行召回：

​ 简单的解释就是，对任一q属于k-reciprocal nearest neightbors, 求R(q,k/2)； 若R(q,k/2)与R(p,k)的交集数量大于2/3的|R(q,k/2)|，则将R(q,k/2)合并到R(p,k)，得到expanded k-reciprocalnearest neightbors.

Jaccard Distance

​ 若probe和gallery的两个图片的k-reciprocal nearest neighbor重叠的越多，可以认为两张图片越近似：

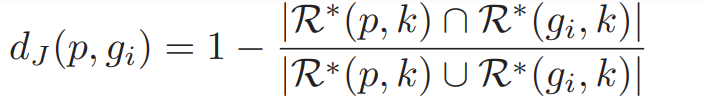
​ 可以使用该距离做为新的度量方式，但是该方法存在几个缺点：

（1）时间复杂度高：

重新计算距离矩阵的复杂度为
$$
O((N+M)^2kk)
$$
N,M分别为probes, galleries的图片数量

计算expanded k-reciprocalnearest neightbors的时间复杂度为：
$$
O((N+M)(D(N+M)+(N+M)+klog(N+M)+kk/2log(N+M)))
$$
其中, D为feature的长度，(N+M)是建堆的时间复杂度，kxlog(N+M)是topk的查询复杂度，kxk/2xlog(N+M))是expand的时间复杂度。

ps: 其实个人理解使用修改后的方案（k-reciprocal feature），还是要计算expanded k-reciprocalnearest neightbors，所以k-reciprocal feature并不是针对这点提出的改进。

（2）jaccard distance未考虑top-k中每张图片的权重，但显然排名高的图像权重应该更大

考虑将k-reciprocal nearest neighbor编码为向量，称为k-reciprocal feature

k-reciprocal feature

即对属于expand k-reciprocal nearest neighbor的编码为1，否则为0，长度为probes+galleries的长度.

接下来，对编码为1的使用指数函数计算相似度：


其中公式（8）（9）可以这样理解，对于一个向量，按元素操作，0和非零值取min代表着交集，0和非零值取max 代表着并集，其一阶范数代表这集合得大小。

Local Query Expansion

假设相同ID的图片拥有相似的特征，因此可以使用probe的topk对Vp进行修正，注意top-k应该包含了p：

Code

reranking 主要有3个参数： k1=20, k2=6, lambda_value=0.3

k1是计算k-reciprocal nearest neighbor的k，不宜过大，特别是存在大量只有几张图片的ID时

k2是计算Local Query Expansion的k, 不宜过大，特别是存在大量只有几张图片的ID时，而且一般比k1小